Navigation, SLAM, and SFM¶

# Install pre-release version of gtsam and gtbook to enable bleeding edge code
# %pip install -q --index-url https://test.pypi.org/simple gtsam==4.2a5
# %pip install -q --index-url https://test.pypi.org/simple gtbook==0.0.17
Overview¶
- Probabilistic Inference
- Navigation/Localization in 1D
- Nonlinear Optimization (sensor networks example)
- Optimization on Manifolds (Pose SLAM)
- Optimization with Landmarks (SLAM, Visual SLAM, and SfM)
- Neural Radiance Fields
References¶
- Talk is online here: https://dellaert.github.io/NavSlamSfmTalk.html
- Colab is here: https://tinyurl.com/NavSlamSfmColab
- Annual Reviews article on factor graphs for this and more: https://t.co/Xc0RMXyeYY
- Neural Radiance Fields blog posts at https://dellaert.github.io/year-archive/
- Factor Graphs for Robot Perception: http://www.cs.cmu.edu/~kaess/pub/Dellaert17fnt.pdf
- The book on Multi-view geometry: Hartley & Zisserman: https://www.robots.ox.ac.uk/~vgg/hzbook/
Probabilistic Inference¶
- Markov Chains
- Dynamic Bayes Nets
- Factor Graphs
- Inference Algorithms
- Applications
Markov Chains¶
Let's use the GTSAM library, which has some built-in support for creating variables over time.¶
# try varying 5. I tried up to 120, but graphics are less useful for large numbers...
N = 5
indices = range(1, N+1)
X = VARIABLES.discrete_series(
character='X', indices=indices, domain=["A", "B", "C"])
VARIABLES
| Variable | Domain |
|---|---|
| X1 | A, B, C |
| X2 | A, B, C |
| X3 | A, B, C |
| X4 | A, B, C |
| X5 | A, B, C |
A Markov chain is specified by a prior $P(X_1)$ on the first state $X_1$ and the transition probability $P(X_{k+1}|X_k)$.¶
markov_chain = gtsam.DiscreteBayesNet()
prior_pmf = "3/1/1"
transition_cpt = "3/2/0 0/3/2 0/0/1"
markov_chain.add(X[1], prior_pmf)
for k in indices[:-1]:
markov_chain.add(X[k+1], [X[k]], transition_cpt)
ROW(pretty(markov_chain.at(j)) for j in range(N))
P(X1):
|
P(X2|X1):
|
P(X3|X2):
|
P(X4|X3):
|
P(X5|X4):
|
We can represent a Markov chain graphically using the language of Bayes nets. The Bayes net is generative, and encodes $$P(\mathcal{X}) = P(X_1) \prod_{k>1} P(X_{k+1}|X_k)$$¶
show_discrete(markov_chain, hints={'X': 1})
We can then use ancestral sampling, e.g. here are some samples:¶
reverse_markov_chain = reverse(markov_chain)
ROW(pretty(reverse_markov_chain.sample()) for j in range(3))
|
|
|
The stationary distribution (you might know it as PageRank) of a Markov chain can be computed using the power method.¶
T = np.array([[0.75, 0.25, 0], [0, 0.75, 0.25],[0, 0, 1]]).transpose()
pi0 = [1,1,1]; pi = [np.array(pi0)/sum(pi0)]
for _ in range(20):
pi.append(T@pi[-1])
px.line(np.array(pi))
Dynamic Bayes Nets¶
Let's add actions $A_k$ and measurements $Z_k$:
A = VARIABLES.discrete_series(
character='A', indices=indices[:-1], domain=["Stay", "Go"])
Z = VARIABLES.discrete_series(
character='Z', indices=indices, domain=["Off", "On"])
VARIABLES
| Variable | Domain |
|---|---|
| X1 | A, B, C |
| X2 | A, B, C |
| X3 | A, B, C |
| X4 | A, B, C |
| X5 | A, B, C |
| A1 | Stay, Go |
| A2 | Stay, Go |
| A3 | Stay, Go |
| A4 | Stay, Go |
| Z1 | Off, On |
| Z2 | Off, On |
| Z3 | Off, On |
| Z4 | Off, On |
| Z5 | Off, On |
Dynamics Bayes nets (DBNs) are a factored generalization of Markov chains. Here we added the actions and measurements to a Markov chain:¶
dbn = gtsam.DiscreteBayesNet()
dbn.add(X[1], prior_pmf)
sensor_cpt = "3/1 1/3 1/3"
action_cpt = "1/0/0 0/1/0 0/0/1 3/2/0 0/3/2 0/0/3"
for k in indices[:-1]: dbn.add(X[k+1], [A[k], X[k]], action_cpt)
for k in indices: dbn.add(Z[k], [X[k]], sensor_cpt)
position_hints = {'A': 2, 'X': 1, 'Z': 0}
show_discrete(dbn, hints=position_hints)
We have an initial prior $P(X_1)$, but now the transition model $P(X_{k+1}|X_k,A_k)$ is action-dependent, and we also have a generative measurement model $P(Z_k|X_k)$.¶
ROW(pretty(dbn.at(j)) for j in [0,N,1])
P(X1):
|
P(Z1|X1):
|
P(X2|A1,X1):
|
Actions and measurements are generally known, and hence we render them as boxes.¶
known = [key[0] for key in list(A.values())+list(Z.values())]
show_discrete(dbn, hints=position_hints, boxes=set(known))
We can sample some measurements given a known "control tape".¶
ROW([pretty(actions), pretty(rollout)])
|
|
Factor Graphs¶
A factor graph only keeps the unknown variables, and puts the narrowed down CPTs in factors. A factor graph encodes the posterior $$\Phi(\mathcal{X})=\prod_i \phi(\mathcal{X}_i)$$ where $\mathcal{X}_i$ is the set of variables connected to factor $\phi_i$.¶
graph = gtsam.DiscreteFactorGraph()
graph.push_back(dbn.at(0))
for k in indices[:-1]: graph.push_back(dbn.at(k).choose(actions)) # action-specific transition
for k in indices:
factor = dbn.at(k+N-1).likelihood(rollout[Z[k][0]]) # measurement-specific likelihood
graph.push_back(factor)
# show_discrete a few factors, you can also try `pretty(graph)`
ROW(pretty(graph.at(i)) for i in [0, N, 1, N+1, 2])
P(X1):
|
|
P(X2|X1):
|
|
P(X3|X2):
|
Factor graphs, unlike Bayes nets, are bipartite graphs:¶
# show_discrete factor graph
pos = {0:(0.35,1)}
pos.update({k:(k+0.5,1) for k in indices[:-1]}) # binary
pos.update({k+N-1:(k,0.5) for k in indices}) # unary
show_discrete(graph, hints=position_hints, factor_positions=pos)
Inference Algorithms¶
- max-product
- sum-product
The max-product algorithm finds the Maximum probable explanation (MPE). In HMMs it is also known as the Viterbi algorithm.¶
pretty(graph.optimize())
| Variable | value |
|---|---|
| X1 | C |
| X2 | C |
| X3 | C |
| X4 | C |
| X5 | C |
Like max-product, the sum-product algorithm (also known as the forward algorithm in HMMs) eliminates one variable at a time:¶
from IPython.display import Latex, Markdown
product = graph.at(N) * graph.at(0) * graph.at(1)
summed = gtsam.DiscreteConditional(1, product)
ROW([pretty(graph.at(0)), pretty(graph.at(1)), pretty(graph.at(5)),
"product:", pretty(product), "sum:", pretty(summed)])
P(X1):
|
P(X2|X1):
|
|
product: |
|
sum: | P(X1|X2):
|
The result is again a Bayes net that encodes the posterior $P(X|Z,A)$, laid out in elimination ordering:¶
posterior = graph.sumProduct()
show_discrete(posterior, hints=position_hints)
ROW(pretty(posterior.at(j)) for j in range(N))
P(X1|X2):
|
P(X2|X3):
|
P(X3|X4):
|
P(X4|X5):
|
P(X5):
|
Bonus: you can eliminate in any ordering, which will become important later on, e.g., nested dissection:¶
metis = graph.sumProduct(OrderingType.METIS); show_discrete(metis)
ROW(pretty(metis.at(j)) for j in range(N))
P(X2|X1,X3):
|
P(X1|X3):
|
P(X5|X4):
|
P(X4|X3):
|
P(X3):
|
Applications¶
- sample
- calculate marginals
Once we have the posterior as a Bayes net, we can sample efficiently from the posterior $P(\mathcal{X}|\mathcal{Z})$:¶
ROW(pretty(posterior.sample()) for j in range(10))
|
|
|
|
|
|
|
|
|
|
Or calculate joints and marginals exactly:¶
# variables names are for N=5
P_X5 = posterior.at(N-1)
P_X4_given_X5 = posterior.at(N-2)
P_X4_X5 = P_X5 * P_X4_given_X5
P_X4 = P_X4_X5.marginal(X[N-1][0])
ROW([P_X4_given_X5, "*", P_X5, "=", P_X4_X5, "=>", P_X4])
P(X4|X5):
|
* | P(X5):
|
= | P(X4,X5):
|
=> | P(X4):
|
We can recursively calculate all marginals in this way, in a backward pass, which is a variant of the forward-backward algorithm in HMMs.¶
Navigation/Localization in 1D¶
- A dynamic Bayes net for navigation
- Factor graph
- Inference = Linear!
Navigation DBN¶
We create gtsam.Symbols now, with lowercase symbols to indicate continuous variables.¶
u = {k:gtsam.symbol('u',k) for k in indices[:-1]} # controls u_k
x = {k:gtsam.symbol('x',k) for k in indices} # states x_k
z = {k:gtsam.symbol('z',k) for k in indices} # measurements z_k
We can construct a Dynamics Bayes nets with continuous densities on vector-valued controls, states, and measurements:¶
gbn = gtsam.GaussianBayesNet()
d = np.zeros((1,1))
R = np.ones((1,1))
gbn.push_back(gtsam.GaussianConditional(x[1], d, R))
for k in indices[:-1]:
gbn.push_back(gtsam.GaussianConditional(x[k+1], d, R, u[k], [-1], x[k], [-1])) # |x+ - x - u|^2
for k in indices:
gbn.push_back(gtsam.GaussianConditional(z[k], d, R, x[k], [-1])) # |z - x|^2
position_hints = {'u': 2, 'x': 1, 'z': 0}
show(gbn, hints=position_hints)
We now have an Gaussian prior $p(x_1)$, a Gaussian motion model $p(x_{k+1}|x_k,u_k)$, and a Gaussian measurement model $p(z_k|x_k)$.¶
XX = np.linspace(-3, 3)
px1 = np.exp(-np.array([gbn.at(0).error(vv({x[1]:[xx]})) for xx in XX]))/np.sqrt(2*np.pi)
px.line(x=XX, y=px1)
Actions and measurements, which are generally known, and hence we render them as boxes.¶
known = [key for key in list(u.values())+list(z.values())]
show(gbn, hints=position_hints, boxes=set(known))
The measurement model conditional Gaussian, but when given a measurement $z_k$ it becomes a 1D likelihood function :¶
given_z = 0.5
Lx1_given_z1 = np.exp(-np.array([gbn.at(N).error(vv({x[1]:[xx], z[1]:[given_z]})) for xx in XX]))
px.line(x=XX, y=Lx1_given_z1)
The motion model, given a control action $u_k$, is a 2D degenerate Gaussian:¶
given_u = 1.0
motion_model = gbn.at(1)
e = np.array([[motion_model.error(vv({x[1]:[xx], x[2]:[yy], u[1]:[given_u]}))
for xx in XX] for yy in XX])
fig = go.Figure(data=go.Contour(x=XX, y=XX, z=np.exp(-e)/(2*np.pi)))
fig.update_yaxes(scaleanchor = "x",scaleratio = 1); fig.show()
Navigation Factor Graph¶
In the continuous case, we build the factors directly from given controls and measurements. A factor graph now encodes the negative log-posterior $$\Phi(X)=\sum_i \phi(X_i) = \frac{1}{2} \sum_i \|A_i X_i-b_i\|^2$$.¶
# build factor graph
controls = {k: 1.0 for k in indices[:-1]} # controls (and measurements) assumed known!
gfg = gtsam.GaussianFactorGraph()
gfg.push_back(gbn.at(0))
for k in indices[:-1]: gfg.push_back(motion_factor(k)) # |x+ - x - u|^2
for k in indices: gfg.push_back(measurement_factor(k)) # |z - x|^2
show(gfg, hints=position_hints, factor_positions=pos)
Inference = Linear¶
Key message:
- factor graph == rectangular matrix
- Bayes net = Cholesky factor
- Ordering matters
A 1D navigation factor graph is a (block-sparse) Jacobian matrix $A$ and right-hand-size $b$:¶
Every row corresponds to a factor, every column to a variable. The last column is the RHS $b$.
# show [A|b]
px.imshow(gfg.augmentedJacobian(), color_continuous_scale='dense')
And we can just solve for the optimal solution, using QR or Cholesky factorization.¶
gfg.optimize()
VectorValues: 5 elements x1: -0.0797583 x2: 0.908302 x3: 1.9619 x4: 3.00254 x5: 3.88559
The upper-triangular (DAG!) Cholesky factor is the Bayes net that encodes the multivariate Gaussian posterior.¶
gaussian_posterior = gfg.eliminateSequential()
show(gaussian_posterior, hints=position_hints)
if hasattr(gaussian_posterior, 'matrix'):
R, d = gaussian_posterior.matrix()
display(px.imshow(R, color_continuous_scale='dense'))
Bonus: you can eliminate in any ordering, e.g., nested dissection, which can be dramatically faster for more densely connected factor graphs:¶
metis_posterior = gfg.eliminateSequential(OrderingType.METIS); show(metis_posterior)
if hasattr(metis_posterior, 'matrix'):
R, d = metis_posterior.matrix(); display(px.imshow(R, color_continuous_scale='dense'))
Nonlinear Optimization¶
Example: Sensor Network Calibration¶
Let's distribute some sensors in a 2D field, and suppose we have a subset of range measurements between them:¶
num_sensors = 10
sn_indices = range(1,num_sensors+1)
sensor_locations = {k:np.random.uniform(-1,1,size=(2,)) for k in sn_indices}
sensor_locations[1] = np.array([0,0])
sensor_locations[2] = np.array([1,0])
range_measurements : dict = {}
for k1 in sn_indices:
for k2 in sn_indices[k1:]:
if np.random.rand()>0.3:
range12 = np.linalg.norm(sensor_locations[k2]-sensor_locations[k1])
range_measurements[k1,k2] = range12 + np.random.normal(scale=0.01)
range_measurements
{(1, 3): 0.6871356824394776,
(1, 4): 0.8929222940253249,
(1, 6): 0.41717229502934344,
(1, 7): 1.0635997091697238,
(1, 8): 0.44509469139046925,
(1, 9): 0.7815009680626832,
(1, 10): 0.9066581553298038,
(2, 3): 0.5223442765799242,
(2, 4): 1.4148558916314318,
(2, 5): 1.4851238121218555,
(2, 6): 0.7370366631818027,
(2, 7): 0.8195056707187741,
(2, 8): 1.4265925474794314,
(2, 9): 1.1793158832568933,
(2, 10): 0.26856382858724875,
(3, 4): 1.421063174668384,
(3, 5): 1.2938221701107113,
(3, 6): 0.30748477369086136,
(3, 7): 0.46879251736780037,
(3, 8): 1.0221642944207665,
(3, 9): 1.2022367913821348,
(4, 5): 0.5890530334203953,
(4, 6): 1.2261816497682487,
(4, 8): 1.0579925533261627,
(4, 9): 0.2271347826303109,
(4, 10): 1.1775534047101668,
(5, 6): 1.0209403806566473,
(5, 8): 0.558038207921151,
(5, 9): 0.6438013561457799,
(5, 10): 1.331637649038145,
(6, 7): 0.648849678349404,
(6, 9): 1.0560401860444544,
(6, 10): 0.7516408280886956,
(7, 8): 1.320013139702082,
(7, 9): 1.6829256679815672,
(8, 9): 1.0543380029334748,
(8, 10): 1.3510827074430791}
We can skip the generative modeling (Bayes nets) and directly create a factor graph for a sensor network with range-only measurements between them. The factors are non-linear: $$\Phi(X)=\sum_i \phi(X_i) = \frac{1}{2} \sum_i \|h_i(X_i)-z_i\|^2$$¶
range_model = gtsam.noiseModel.Unit.Create(1)
s = {k:gtsam.symbol('s',k) for k in sn_indices}
sensor_network_graph = gtsam.NonlinearFactorGraph()
for k1,k2 in range_measurements:
sensor_network_graph.push_back(gtsam.RangeFactor2(s[k1], s[k2],
range_measurements[k1,k2], range_model))
ground_truth_locations = gtsam.Values()
for k, pos in sensor_locations.items(): ground_truth_locations.insert(s[k],pos)
show(sensor_network_graph, ground_truth_locations, binary_edges=True)
Gauss-Newton Optimization¶
Because the system is nonlinear, we can repeatedly linearize all non-linear factors and optimize the resulting linear factor graph, until convergence. This vanilla scheme is called Gauss-Newton, and linearizes by $$\sum_i \|h_i(X^t_i+\delta_i)-z_i\|^2 \approx \sum_i \|h_i(X^t_i) + H_i \delta_i -z_i\|^2$$¶
initial = gtsam.Values()
for k in sn_indices: initial.insert(s[k],np.random.uniform(-1,1,size=(2,)))
optimizer = gtsam.GaussNewtonOptimizer(sensor_network_graph, initial)
try:
optimizer.optimize()
except:
print("Indeterminant linear system detected!")
Indeterminant linear system detected!
We need to add a multiple priors to make the problem observable, because there is an $SE(2)$ "gauge freedom".¶
prior_model = gtsam.noiseModel.Isotropic.Sigma(2, 0.1)
sensor_network_graph.addPriorPoint2(s[1],sensor_locations[1], prior_model)
sensor_network_graph.addPriorPoint2(s[2],sensor_locations[2], prior_model)
show(sensor_network_graph, ground_truth_locations, binary_edges=True)
With priors, the system might converge. There can still be under-determined sensors. Guess why! But even if not, Gauss-Newton can diverge quickly.¶
initial = gtsam.Values()
for k in sn_indices: initial.insert(s[k],np.random.uniform(-1,1,size=(2,)))
optimizer = gtsam.GaussNewtonOptimizer(sensor_network_graph, initial)
errors = [optimizer.error()]
for it in range(1,10):
try:
optimizer.iterate()
except:
print("Indeterminant linear system detected!")
errors.append(optimizer.error())
px.line(errors)
Levenberg-Marquardt¶
One approach is to add priors to all variables if we detect divergence, so the optimizer does not jump beyond a certain "trust region". The simple prior scheme is called Levenberg-Marquardt, after its inventors.¶
LM = gtsam.LevenbergMarquardtOptimizer(sensor_network_graph, initial)
errors = [LM.error()]
for it in range(1,10):
LM.iterate()
errors.append(LM.error())
px.line(errors)
Comparing the ground truth with the low-error, optimized (maximum a posteriori) solutions can still lead to surprises.¶
map_locations = LM.values()
data = {"GT":np.array(list(sensor_locations.values())),
"MAP":np.stack([map_locations.atPoint2(s[k]) for k in sn_indices])}
plots=[go.Scatter(x=data[l][:,0], y=data[l][:,1], name=l) for l in ['GT','MAP']]
fig = go.Figure(data=plots)
fig.update_yaxes(scaleanchor = "x",scaleratio = 1)
fig.show()
GPS-Like navigation¶
GPS is based on range to satellites with known position. A 2D, GPS-like navigation example combines the example above with odometry.¶
# build factor graph with range measurements to s1 and s2
gps_graph = gtsam.NonlinearFactorGraph()
gps_graph.addPriorPoint2(x[1],[0,0], prior_model)
motion_model = gtsam.noiseModel.Isotropic.Sigma(2,1)
for k in indices[:-1]:
gps_graph.push_back(gtsam.BetweenFactorPoint2(x[k], x[k+1], [1,0], motion_model)) # motion model
for k in indices:
simulated = gtsam.Point2(0,k-1)
for i in [1,2]:
range_ks = np.linalg.norm(simulated - sensor_locations[i])
gps_graph.push_back(gtsam.RangeFactor2(x[k], s[i], range_ks, range_model)) # range measurement
position_hints.update({'s':2})
show(gps_graph, gtsam.Values(), hints=position_hints, binary_edges=True)
We use Levenberg-Marquardt to optimize the entire trajectory at once.¶
initial = gtsam.Values()
initial.insert(s[1], sensor_locations[1])
initial.insert(s[2], sensor_locations[2])
for k in indices: initial.insert(x[k],np.random.uniform(-1,1,size=(2,)))
LM = gtsam.LevenbergMarquardtOptimizer(gps_graph, initial)
errors = [] # don;t show initial error (very large)
for it in range(1,10):
LM.iterate()
errors.append(LM.error())
map_trajectory = LM.values()
px.line(errors)
The optimized trajectory.¶
data = {"initial":np.stack([initial.atPoint2(x[k]) for k in indices]),
"MAP":np.stack([map_trajectory.atPoint2(x[k]) for k in indices])}
plots=[go.Scatter(x=data[l][:,0], y=data[l][:,1], name=l) for l in ['initial','MAP']]
fig = go.Figure(data=plots)
fig.update_yaxes(scaleanchor = "x",scaleratio = 1)
fig.show()
Optimization on Manifolds¶
- Motivation
- Pose SLAM
- The Bayes Tree
Motivation¶
Robots/vehicles frequently operate in $SE(2)$, the space of 2D poses combining 2D position with a 1D orientation. This is a manifold, not a vector space, so we cannot add. We define a retraction $\Psi$:¶
E.g., for $g\in SE(2)$, an example retraction is the exponential map: $$\Psi(g, \delta) = g \exp(\hat{\delta})$$ where $\delta\in R^3$ is a 3-vector, and $\hat{\delta}$ is an element of the Lie algebra $\mathfrak{se(3)}$.
pose = gtsam.Pose2(2,3, 0.5)
print(f"pose = {pose}")
print(f"pose.retract([1,1,1]) = {pose.retract([1,1,1])}")
print(f"pose.retract([1,1,6]) = {pose.retract([1,1,6])}")
pose = (2, 3, 0.5) pose.retract([1,1,1]) = (2.39816, 4.35701, 1.5) pose.retract([1,1,6]) = (2.39816, 4.35701, 0.216815)
That seems scary, but for the 3D rotations $R\in SO(3)$, the quantity $\delta$ behaves like an angular velocity $\omega$, and the quantity $\hat{\delta}$ is just a skew-symmetric matrix $[\omega]$.
Probably the most illustrative example is the sphere $S^2$ in $R^3$ (Unit3 in GTSAM), which is useful in dealing with phone orientation etc...¶
base = gtsam.Unit3([-1,1,1])
Delta = np.random.uniform(-1.5, 1.5, size=(1000,2))
Ts = Delta @ base.basis().T + base.point3()
Us = [base.retract(delta) for delta in Delta]
Ps = np.array([unit3.point3() for unit3 in Us])
fig = go.Figure()
fig.add_trace(go.Scatter3d(x=Ts[:,0], y=Ts[:,1], z=Ts[:,2], mode="markers", marker=dict(size=2, color="red"), showlegend= False))
fig.add_trace(go.Scatter3d(x=Ps[:,0], y=Ps[:,1], z=Ps[:,2], mode="markers", marker=dict(size=2, color="green"), showlegend= False))
fig.update_layout(margin=dict(l=0, r=0, t=0, b=0))
fig.update_yaxes(scaleanchor = "x", scaleratio = 1); fig.show()
Manifold variants of Gauss-Newton and Levenberg-Marquardt¶
Linearization now includes establishing tangent spaces around current solution, and using the Jacobians from the tangent space to the error.¶
- Every factor $\phi_i$ now contains a function $h_i(X_i)$ from a set of manifold variables $X_i$ to a vector.
- Linearize: $$\sum_i \|h_i(\Psi(X^t_i, \delta_i))-z_i\|^2 \approx \sum_i \|h_i(X^t_i) + H_i \delta_i -z_i\|^2$$
- Solve linear system with $\delta$ vectors $\rightarrow \delta^*$
- Update linearization point with retraction: $$X^{t+1}_i = \Psi(X^t_i, \delta^*_i)$$
Example: Pose SLAM¶
Pose SLAM just has 2D poses as unknowns, and relative pose measurements that can be derived from odometry or LIDAR scan matching, or both in many cases¶
# Create noise models
PRIOR_NOISE = gtsam.noiseModel.Diagonal.Sigmas(gtsam.Point3(0.3, 0.3, 0.1))
ODOMETRY_NOISE = gtsam.noiseModel.Diagonal.Sigmas( gtsam.Point3(0.2, 0.2, 0.1))
Between = gtsam.BetweenFactorPose2
pose_slam_graph = gtsam.NonlinearFactorGraph()
pose_slam_graph.add(gtsam.PriorFactorPose2(1, gtsam.Pose2(0, 0, 0), PRIOR_NOISE))
pose_slam_graph.add(Between(1, 2, gtsam.Pose2(2, 0, 0), ODOMETRY_NOISE))
pose_slam_graph.add(Between(2, 3, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE))
pose_slam_graph.add(Between(3, 4, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE))
pose_slam_graph.add(Between(4, 5, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE))
pose_slam_graph.add(Between(5, 2, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE)) # loop closure
Let's check out the factor graph in this case, with an OK initial estimate:¶
initial_estimate = gtsam.Values()
initial_estimate.insert(1, gtsam.Pose2(0.5, 0.0, 0.2))
initial_estimate.insert(2, gtsam.Pose2(2.3, 0.1, -0.2))
initial_estimate.insert(3, gtsam.Pose2(4.1, 0.1, math.pi / 2))
initial_estimate.insert(4, gtsam.Pose2(4.0, 2.0, math.pi))
initial_estimate.insert(5, gtsam.Pose2(2.1, 2.1, -math.pi / 2))
show(pose_slam_graph, initial_estimate, binary_edges=True)
In this case, with a good initial estimate, Gauss-Newton does OK¶
parameters = gtsam.GaussNewtonParams()
parameters.setRelativeErrorTol(1e-5)
parameters.setMaxIterations(100)
optimizer = gtsam.GaussNewtonOptimizer(pose_slam_graph, initial_estimate, parameters)
pose_slam_result = optimizer.optimize()
We can show marginals as (2.5 $\sigma$) ellipses:
marginals = gtsam.Marginals(pose_slam_graph, pose_slam_result)
for i in range(1, 6):
gtsam_plot.plot_pose2(0, pose_slam_result.atPose2(i), 0.5,
marginals.marginalCovariance(i))
plt.axis('equal'); plt.show()
Larger Pose SLAM Example¶
Here we read from a "g2o" file to show off a larger example.¶
g2oFile = gtsam.findExampleDataFile("w10000.graph")
manhattan_graph, initial = gtsam.load2D(g2oFile,
noiseFormat=gtsam.NoiseFormat.NoiseFormatTORO, maxIndex=3000)
manhattan_graph.add(gtsam.PriorFactorPose2(0, gtsam.Pose2(), PRIOR_NOISE))
show(manhattan_graph, initial, binary_edges=True) # < takes a bit
Despite having 3000 poses to optimize, Levenberg Marquardt eats through this in less than a second.¶
%%time
optimizer = gtsam.LevenbergMarquardtOptimizer(manhattan_graph, initial)
manhattan_result = optimizer.optimize()
CPU times: user 740 ms, sys: 37.1 ms, total: 777 ms Wall time: 775 ms
resultPoses = gtsam.utilities.extractPose2(manhattan_result)
fig = px.line(x=resultPoses[:,0], y=resultPoses[:,1])
fig.update_yaxes(scaleanchor = "x",scaleratio = 1); fig.show()
The Bayes tree¶
The Bayes tree captures the cliques of the triangulated Bayes net that encodes the posterior. The cliques always form a tree, and underly multifrontal QR/Cholesky computations.¶
manhattan_graph, initial = gtsam.load2D(g2oFile,
noiseFormat=gtsam.NoiseFormat.NoiseFormatTORO, maxIndex=12)
manhattan_graph.add(gtsam.PriorFactorPose2(0, gtsam.Pose2(), PRIOR_NOISE))
manhattan_gfg = manhattan_graph.linearize(manhattan_result)
ordering = gtsam.Ordering.MetisGaussianFactorGraph(manhattan_gfg)
manhattan_gbn = manhattan_gfg.eliminateSequential(ordering)
manhattan_gbt = manhattan_gfg.eliminateMultifrontal(ordering)
ROW([show(manhattan_gbn), show(manhattan_gbt)])
The Marginals data structure internally re-linearizes and re-solves with the last solution, building a Bayes tree in which a generalization of the forward-backward algorithm is used to calculate marginals (in the tangent space).¶
ROW([show(posterior), "= generalize F/B to tree =>", show(manhattan_gbt)])
| = generalize F/B to tree => |
Optimization with Landmarks¶
- Planar SLAM
- A Larger SLAM Example
- Visual SLAM
- Structure from Motion
Planar SLAM¶
So far we optimized over one type of variable, but often we build a landmark map simultaneously with the trajectory, i.e., this is true SLAM.¶
Let's create a small factor graph with 3 poses and 2 landmarks:
slam_graph = gtsam.NonlinearFactorGraph()
slam_graph.add( gtsam.PriorFactorPose2(x[1], gtsam.Pose2(0.0, 0.0, 0.0), PRIOR_NOISE))
slam_graph.add(Between(x[1], x[2], gtsam.Pose2(2.0, 0.0, 0.0), ODOMETRY_NOISE))
slam_graph.add(Between(x[2], x[3], gtsam.Pose2(2.0, 0.0, 0.0), ODOMETRY_NOISE))
# Add Range-Bearing measurements to two different landmarks L1 and L2
MEASUREMENT_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.1, 0.2]))
BR = gtsam.BearingRangeFactor2D
l = {k:gtsam.symbol('l',k) for k in [1,2]} # name landmark variables
slam_graph.add(BR(x[1], l[1], gtsam.Rot2.fromDegrees(45),np.sqrt(4.0 + 4.0), MEASUREMENT_NOISE)) # pose 1 -*- landmark 1
slam_graph.add(BR(x[2], l[1], gtsam.Rot2.fromDegrees(90), 2.0,MEASUREMENT_NOISE)) # pose 2 -*- landmark 1
slam_graph.add(BR(x[3], l[2], gtsam.Rot2.fromDegrees(90), 2.0,MEASUREMENT_NOISE)) # pose 3 -*- landmark 2
When we have an initial estimate, we can look at the structure of this factor graph:¶
slam_initial = gtsam.Values()
slam_initial.insert(x[1], gtsam.Pose2(-0.25, 0.20, 0.15))
slam_initial.insert(x[2], gtsam.Pose2(2.30, 0.10, -0.20))
slam_initial.insert(x[3], gtsam.Pose2(4.10, 0.10, 0.10))
slam_initial.insert(l[1], gtsam.Point2(1.80, 2.10))
slam_initial.insert(l[2], gtsam.Point2(4.10, 1.80))
show(slam_graph, slam_initial, binary_edges=True)
We optimize again with LM, and show marginals¶
optimizer = gtsam.LevenbergMarquardtOptimizer(slam_graph, slam_initial)
slam_result = optimizer.optimize()
marginals = gtsam.Marginals(slam_graph, slam_result)
for k in [1,2,3]:
gtsam_plot.plot_pose2(0, slam_result.atPose2(x[k]), 0.5, marginals.marginalCovariance(x[k]))
for j in [1,2]:
gtsam_plot.plot_point2(0, slam_result.atPoint2(l[j]), 'g', P=marginals.marginalCovariance(l[j]))
plt.axis('equal'); plt.show()
A Larger SLAM Example¶
Below we optimize a piece of the (old) Victoria park dataset, the factor graph for which is shown below:¶
datafile = gtsam.findExampleDataFile('example.graph')
model = gtsam.noiseModel.Diagonal.Sigmas([0.05,0.05,2*math.pi/180])
[graph,initial] = gtsam.load2D(datafile, model)
priorMean = initial.atPose2(40)
priorNoise = gtsam.noiseModel.Diagonal.Sigmas([0.1,0.1,2*math.pi/180])
graph.addPriorPose2(40, priorMean, priorNoise)
show(graph,initial, binary_edges=True)
Optimizing with LevenbergMarquardtOptimizer, again...¶
initial_poses = gtsam.utilities.extractPose2(initial)
for i in range(initial_poses.shape[0]):
initial.update(i, initial.atPose2(i).retract(np.random.normal(scale=0.5,size=(3,))))
optimizer = gtsam.LevenbergMarquardtOptimizer(graph, initial)
result = optimizer.optimize()
initial_poses = gtsam.utilities.extractPose2(initial)
fig = go.Figure()
fig.add_scatter(x=initial_poses[:,0], y=initial_poses[:,1], name="initial", marker=dict(color='orange'))
final_poses = gtsam.utilities.extractPose2(result)
fig.add_scatter(x=final_poses[:,0], y=final_poses[:,1], name="optimized", marker=dict(color='green'))
fig.update_yaxes(scaleanchor = "x",scaleratio = 1); fig.show()
Visual SLAM¶
Visual SLAM is almost the same problem, but we use 3D poses and 3D points. This is a typical pipeline on drones, phones, etc, everything with an IMU.¶
position_hints.update({'v':2})
show(imu_graph, gtsam.Values(), hints=position_hints)
The factor graph now includes variables for velocity and IMU bias.
We can optimize even without any external measurements, but unless you pay a LOT, your estimate will drift very rapidly.¶
i = 0
while imu_initial.exists(X(i)):
gtsam_plot.plot_pose3(0, imu_initial.atPose3(X(i)), 1)
i += 1
plt.title("imu_initial")
gtsam.utils.plot.set_axes_equal(0)
i = 0
while imu_result.exists(X(i)):
gtsam_plot.plot_pose3(1, imu_result.atPose3(X(i)), 1)
i += 1
plt.title("imu_result")
gtsam.utils.plot.set_axes_equal(1)
Structure from Motion¶
Structure from Motion, or SfM, is the problem of reconstructing 3D structure from multiple images, even when taken from different cameras or at different times.¶

SfM is almost the same problem as Visual SLAM, but typically there is no odometry between cameras. The optimization problem is also called Bundle Adjustment. Arguably, the most difficult problem associated with SfM is feature detection, data association, and initializing the optimization.¶
# Load data from file and create factor graph and initial estimate
filename = gtsam.findExampleDataFile("Balbianello.out")
sfm_data = gtsam.SfmData.FromBundlerFile(filename)
model = gtsam.noiseModel.Isotropic.Sigma(2, 1.0) # one pixel in u and v
graph = sfm_data.sfmFactorGraph(model)
initial = gtsam.initialCamerasAndPointsEstimate(sfm_data)
print(f"initial error: {graph.error(initial)}")
initial error: 126.92834251964683
# Optimize
try:
lm = gtsam.LevenbergMarquardtOptimizer(graph, initial)
result = lm.optimize()
except RuntimeError:
print("LM Optimization failed")
print(f"final error: {graph.error(result)}")
final error: 125.51738267205192
The result of SfM is a sparse point cloud and a set of well-determined camera poses and camera calibration, which can be densified using multiview-stereo techniques.¶
# Get points, filter them, and display with plotly
structure = gtsam.utilities.extractPoint3(result)
valid = structure[:,2] > -5.0
bRc = sfm_data.camera(0).pose().rotation()
wRc = gtsam.Rot3([1,0,0],[0,0,-1],[0,1,0]) # make camera point to world y
wRb = wRc.compose(bRc.inverse())
structure = (wRb.matrix() @ structure.T).T
fig = go.Figure()
fig.add_trace(go.Scatter3d(x=structure[valid,0],y=structure[valid,1],z=structure[valid,2],
mode="markers", marker=dict(size=2, color="blue"), showlegend= False))
fig.update_layout(margin=dict(l=0, r=0, t=0, b=0))
fig.update_yaxes(scaleanchor = "x", scaleratio = 1); fig.show()
Neural Radiance Fields¶
NeRF, or neural radiance fields, is the latest and greatest in densifying (literally, estimating a density field) and synthesizing new views from the scene. See "NeRF Explosion 2020"¶
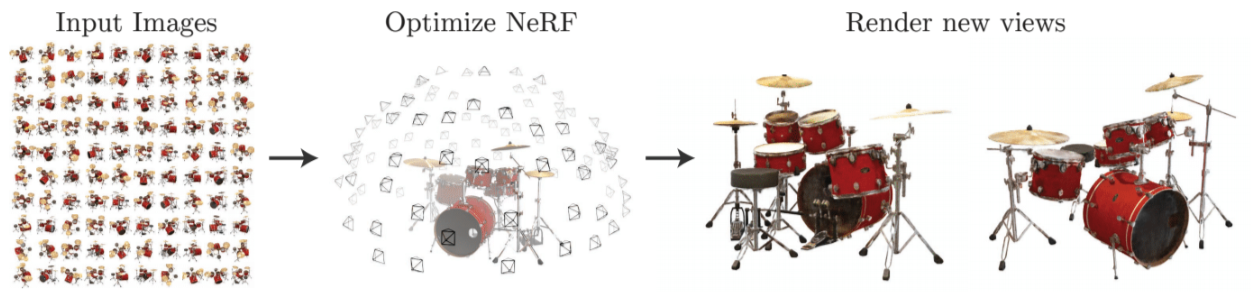
A NeRF stores a volumetric scene representation as the weights of an MLP, trained on many images with known pose.
NeRF can even be used to refine the pose of images.¶
iNeRF teaser GIF: iNERF uses NeRF as a synthesis model in a pose optimizer.
Or even doing the whole SfM process from scratch, see NeRF at ICCV 2021, e.g., below: NeRF on the left, BARF on the right.¶
HTML("""<video width = 900 controls>
<source src="https://chenhsuanlin.bitbucket.io/bundle-adjusting-NeRF/videos2/blender_cams3.mp4" type="video/mp4">
</video>""")
Summary¶
- Probabilistic graphical models underly everything
- Linear least squares is the key underlying computation
- Nonlinear optimization (GN and LM) repeatedly linearize
- Optimization on manifolds needs extra care
- SLAM, Visual SLAM, and Structure from Motion use all of the above
- NeRF is pretty cool :-)
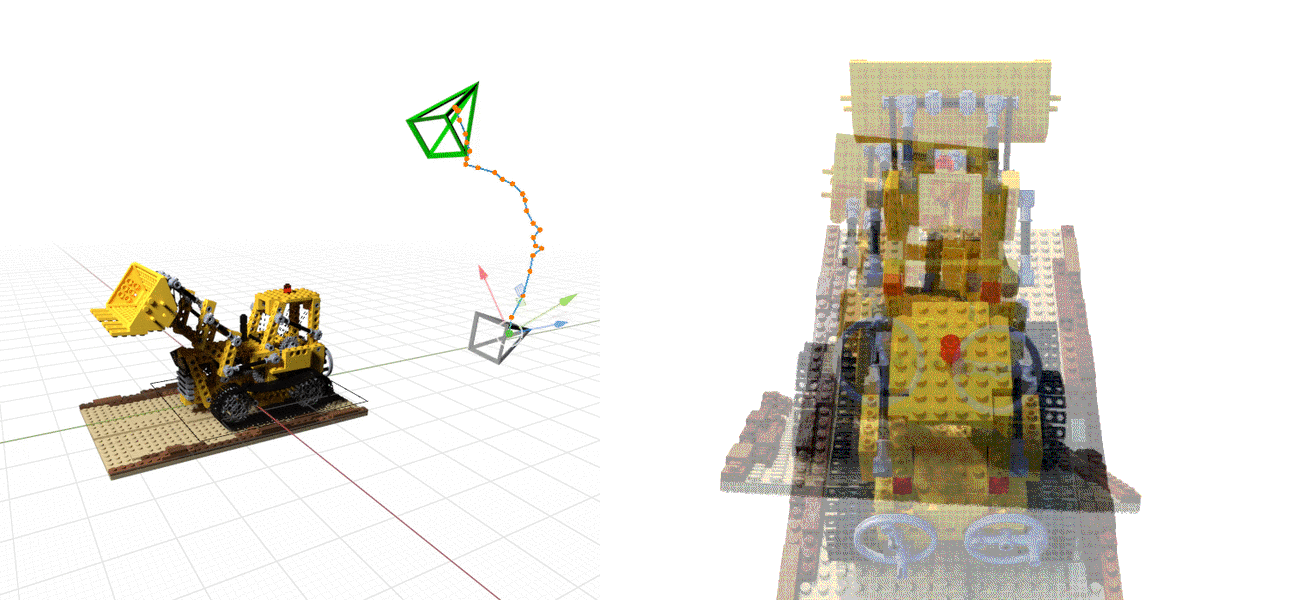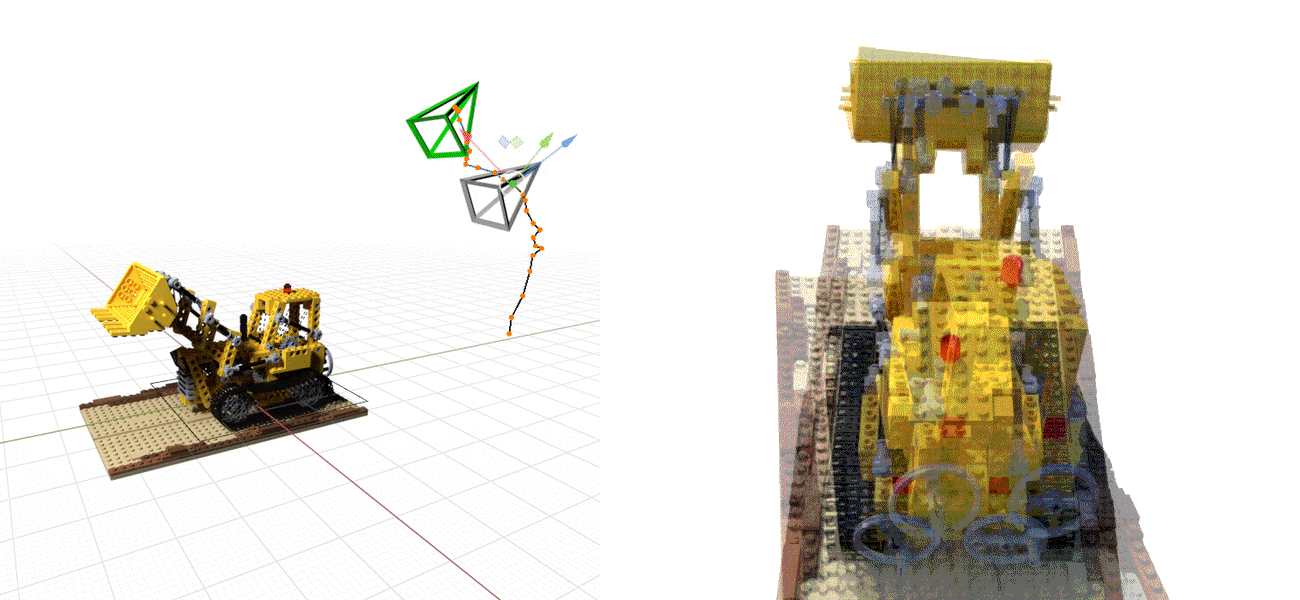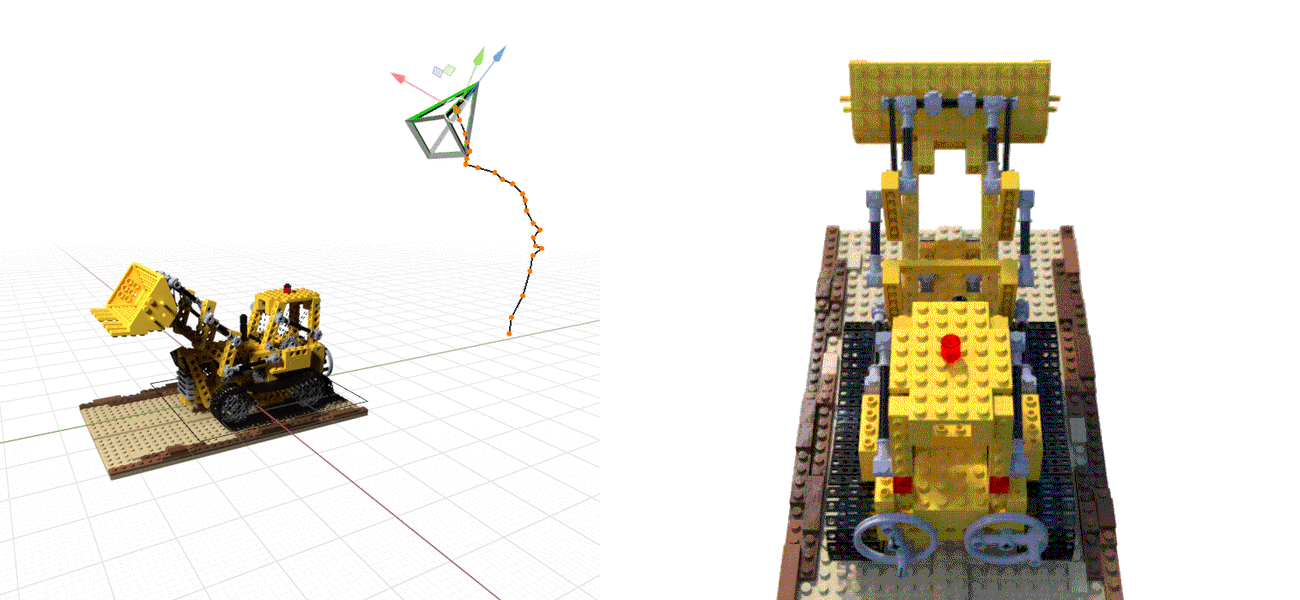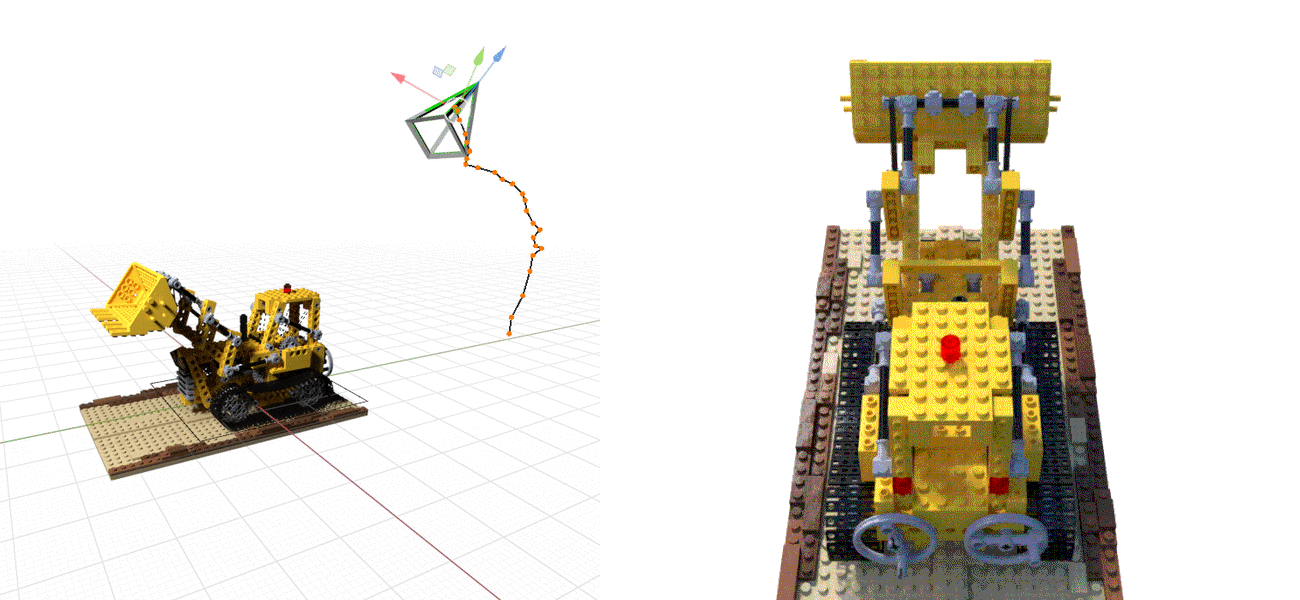 The
The